Introduction to Cryptography, Blade Runner Style

On 7 March 2024, I introduced CryptoTools for the first time in a talk to the local DEFCON group DC608 in Madison, Wisconsin. While I was building the tool in the months prior, I asked lots of people for feedback. From folks unfamiliar with cryptography, the most common feedback I received was, “CryptoTools looks great, but what do I do with it?” I quickly realized that a primer on cryptography was warranted if I wanted to extend its reach.

Storytelling is one of the most powerful methods for conveying ideas and building understanding. For complicated topics like cryptography, I thought that integrating cryptography applications in a story could facilitate engagement and comprehension. I have never been much of a storyteller, so I thought I’d give it a go.

There is a sort of imagery associated with hacker culture. To illustrate the point, I asked ChatGPT 4 to “Generate an image in the style of hacker culture.” It then generated a prompt for DALL•E:

An abstract digital landscape representing the essence of hacker culture, with glowing neon lines on a dark background, symbolizing the flow of information through cyberspace. Silhouettes of hooded figures are subtly integrated, standing before holographic displays filled with code and hacking tools. The atmosphere is electrifying, with hints of futuristic cities and networks in the background, showcasing a blend of technology and mystery.

The result:

I don’t love it. But I might as well own it. A movie came immediately to mind that has compatible imagery: Blade Runner. So here we are.

First, a primer Link to heading

Cryptographic controls, I think, make more sense in the context of an overarching model. In cybersecurity, a common model taught is the so-called CIA Triad, a triangle with Confidentiality, Integrity, and Availability at its nodes. I don’t find this to be an especially useful model. Instead, I prefer the Parkerian Hexad:

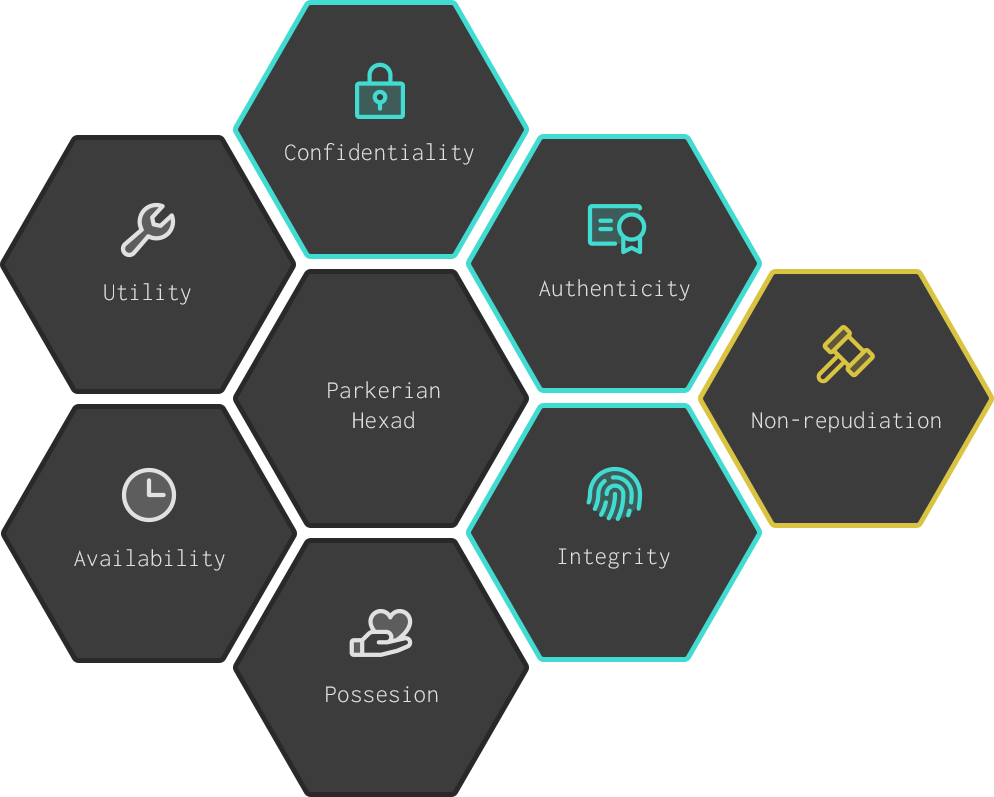
It extends the CIA Triad into a hexagon with nodes Authenticity, Possession, and Utility. Collectively, these are the assurances that cybersecurity should provide.

Cryptography can be used to assure a few of these:

• Authenticity: The assurance that information is sourced from or authored by an intended party, and that no forgery has occurred.
• Confidentiality: The assurance that information is not disclosed to unauthorized parties.
• Integrity: The assurance that information is complete and unaltered, whether deliberately or by accident.

Non-repudiation is not part of the Parkerian Hexad but is a corollary of Authenticity and Integrity. If cryptography is used to ensure that a message was authored by a specific party, and that it was not modified in any way, then it would be difficult for the author to claim that they did not author the message. It’s more of a legal concept, and cryptography cannot usually ensure that a party cannot repudiate the authorship of a message on its own, but it does help.

In a nutshell, cryptography ensures secure communication in the presence of adversarial behavior. Without an adversary, there is no need for cryptography.

On to the story…

Setting Link to heading

The year is 2199 and the replicants have taken control of Earth. The humans are fighting back. Commander Alice and Soldier Bob are preparing to liberate the city of angels, but Eve, a notorious replicant, is doing everything she can to disrupt their plan. (Here Eve lurks in the background.)

How can Alice and Bob communicate safely, knowing Eve is likely listening? How can they ensure their confidentiality?

With encryption.

Confidentiality Link to heading

Encryption is perhaps the most widely known application of cryptography, going all the way back to ancient times. The first practical use is ensuring the secrecy of information in the presence of an eavesdropper. The second practical use is data erasure (just encrypt the data and throw away the key.)

Encryption works by encoding a plaintext message to ciphertext using a key. Decryption is just the same process, in reverse.

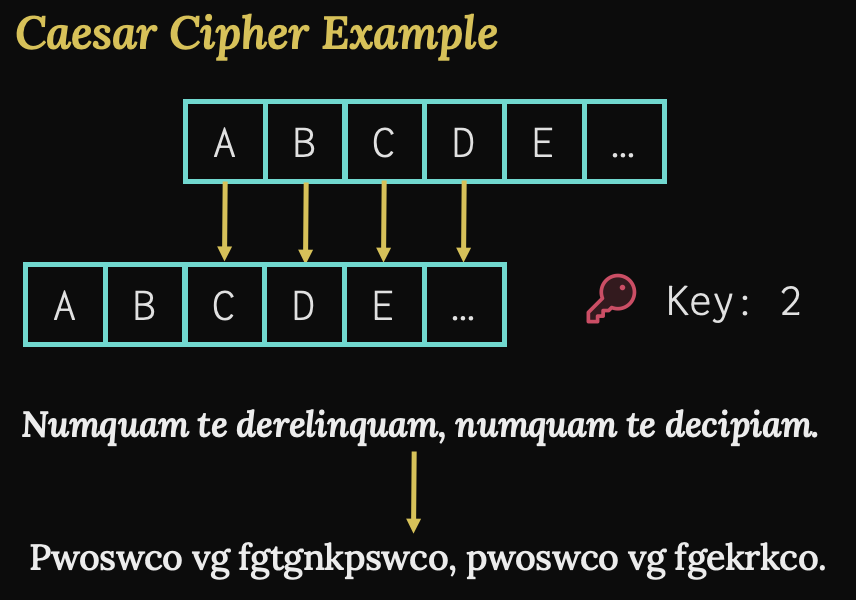
In ancient times, substitution ciphers were used, where the key was a map from one alphabet of symbols to another. Simpler substitution ciphers were also employed, like the famous Caesar Cipher, which shifted the symbols in an alphabet by some fixed number; thus, this number was the key. Here we have an example of a Caesar Cipher using a key of 2 to encrypt a Latin expression I’m sure Caesar used quite frequently.

In modern times we have two types of encryption based on key type. The first is symmetric encryption, where the same key is used to encrypt and decrypt data. Examples of these algorithms include AES (Rijndal), ChaCha20, Blowfish, TwoFish, IDEA, and 3DES. Symmetric key encryption can use either stream or block ciphers. In stream ciphers, bytes or symbols are encrypted one at a time. Caesar Cipher and other substitution ciphers are examples of stream ciphers and are vulnerable to frequency analysis. In block ciphers, data are grouped together into blocks of fixed length. For instance, AES uses 128-bit block sizes.

There are two essential properties of encryption: Confusion and Diffusion. The goal of confusion is to mitigate the probability that an adversary could succeed in determining the secret message. Substituting symbols is a common step in a transformation that accomplishes confusion. Diffusion seeks to spread the plaintext information widely over the ciphertext to mitigate frequency analysis and other forms of pattern recognition. Transposition is a common step in achieving diffusion.

The second type of encryption is asymmetric and is often called public key encryption, which uses more than one key. Examples include RSA, Elliptic Curve Cryptography, and Diffie Hellman. There are some instances where public key encryption is used for confidentiality. RSA in Optimal Asymmetric Encryption Padding mode, for example, can be used to encrypt and decrypt messages. Diffie Hellman Key Exchange is another example of an asymmetric encryption that ensures the confidentiality of a symmetric key in transit. Symmetric ciphers are much more efficient than public key ciphers at encrypting data of large size. Therefore, public key cryptography is used most often for the confidentiality of small amounts of data, or for other assurances like authenticity.

The diagrams here show the difference in how encryption and decryption occur between symmetric and public key encryption. A single secret key is used in the symmetric approach, but two keys are used in the asymmetric approach. The public key encrypts data, and the private key decrypts. If two people want to use asymmetric encryption to securely communicate with one another, they need four keys in total. They each must generate a key pair and exchange their public keys, keeping their private keys secure.

The Secret Link to heading

Commander Alice is ready to communicate a vital secret to Soldier Bob, but she cannot risk Replicant Eve knowing. She decides to generate an AES key with a key length of 256 bits. She chooses Galois Counter Mode because in addition to confidentiality, this mode also provides integrity of the data. That way, Alice can be sure that Eve won’t succeed at viewing the message or modifying portions of it in transit.

There’s just one problem: How does Alice get Bob the key? Since they can’t risk Eve discovering the key, Alice writes it down and folds it into an origami chicken, leaving it in an inconspicuous location for Bob to find. Since chickens have special meaning to him, Bob has no trouble understanding its significance. Later, a courier delivers the message.

Now that Bob has both the key and the ciphertext, he can decrypt the secret message.

Alice’s Secret Key

Algorithm:  AES-256 in Galois Counter Mode
Key: nRp3WQkFI6j09RsQXc83QkSplfwtB/N7wzd1cyGC++A=

Initialization Vector (IV) (not secret)

7hhLFq9gN0HAKVir

Ciphertext

FamBdpl+eLgzjNWWqmX7f7GSkA+VC33KNlrdw2v0X3K+0mE9DJ64JtCvhi/bfZO760NToZfIYPj4Eh61BVPTd/o8g9D9Hl2GcKlg/pKf55ZHR6/06TZo4L708+00gKoaeXv9egGkY3WhpMBlFa+v+dV9VO8Su/I6TuHjX3aqi0M6pvjgvGjhecM2JR3ctNsGZlhpU9R0rHrC/igDhcKurT3ZN6MtrhrJW2uc6qhNNp24uH4aAsXzOkI1szMbUrG8APy4pmUM3qehF9fTu80b65qIFS5DzreHZs3zC68SYNK+dEwqLi0VcVaNxWWVddZZjueVypMmmWmsiZPFM5QLw2RZ3cNGAPoo23VJ7hJNYJBzKCvuFQ8pbPTeEY75YVlqViO7aIjuuXWNvaWzu73YHNj+1lfCwEI1mvrRsV568e/oakp39ME3u3MX09dJNin5uM+ijZ7cEJLgRd/PZlB/nPc7DquXPN4HdBsgBVsg5e/fEDz7KaMnLJgSQ1Ept+a+NByEUWwx/EynJm6dnnyZoLMIUM2tGjCwMSeVbMk3tpeRJcVv4S3Mmx9dAE1rk6JBPU7Dhd8Y4XeNr6v3XNesbyF6Ca7DWoaoqsZ6gYzvi7yNHUJlCBXcInLagzF3PF3C+dLEGBDPU52lP97/DGqDtGj6egXBIwZjyYHiG23Qw9QTpy+OlnVZZLqoImQObYDRXizZ6eQiJNVWPakSHySe9i3ELkNLupLt6as0qt2UJovbM/YRYMwQgzeiZt7Ul8T/l8Aqcks04rsKvfm1UeURHiCD22j9fWOUQ6p3JyfIUj8vKdJJ/KYVYY5TQpXyzuYAxAAlG6h2geuWDlfN67JaSPpWOksSsTFTnaBSsjqzCz1EpGvAYHQUR9xTKQJPaGK0aGc01qz2h2iacssdLU03VWwGOVc0Fk68EyOd+d7/GQLw2zcZ2P1INk5iN14yLhEuow6rgoOayDWdmF0fnHkgUm+kPRI4aGsGc3ICg0wFa/fcTXKIBHyzXs9ZHTRcTGEGxf4CGM3zvD0d0lWarfMhYiRu8owvcMxtNmjcqQdZ5K2wLnTleUfg59ertrHYzp09Khy7E/f4puAyANaOSDYja2HnlG6Ny8LE0Bi0+yVBlz5dd3sA5laxWVgZJt3SymtB/NYI0U70HQpsePlQqgVEVKJe0cpuxKKPsNk=

Try decrypting the message yourself! Go to https://cryptotools.dev > Encryption > Import Key. Check the “Save Locally” box if you want the key to persist through page refreshes. Leave the default algorithm selection as AES GCM. Then, select the newly imported key from the key list, go to the Decrypt tab, paste the ciphertext and the IV into their respective fields. Then click Decrypt.

Bob uses Alice’s secret key to decrypt the secret message:

Soldier Bob, listen closely, for our survival depends on it.

J.F. Sebastian, the genetic designer from the Tyrell Corporation, secretly
placed a backdoor in the genetic code of the replicants. A specific visual
sequence can cause a "biological bit flip" in the lifespan gene of a
replicant, negating its value. This has never been tested before, but we
suspect the consequence to be immediate "retirement" for all replicants
who gaze upon the captivating visual sequence. No need for those lousy
Voight-Kampff tests.

This is the only chance we have left. A payload will be delivered to you
containing this weakness. You must break into the central media station and
upload it to the mainframe to deploy on all displays across the city. Wait
for my command. Trust no one.

The SHA-256 Hash of the payload is:
820a585de241523f7da40c0dcbc42228f39460b3f627d109873952c0e3c83e62

Wait for her command. Trust no one? How dire!

Bob will soon receive the payload. But Eve could intercept it and modify it arbitrarily, rendering it corrupt or ineffective. How can Bob ensure the integrity of the payload?

He can use a cryptographic hash function.

Integrity Link to heading

A hash function takes as input a message of any length, even zero, and produces a deterministic fixed-length output called a Digest; a single message will always produce the exact same digest. In this example, we use SHA-1 as our hash function, which produces digests with a length of 160 bits.

For a hash function to be a cryptographic hash function, it must have at least three essential properties. The first is called pre-image resistance. Eve should be unable to determine the original message from the digest alone. This property makes the hash function a one-way function.

The second property is called second pre-image resistance. Even if Eve has the message and its digest, it should be very difficult to discover some other message that produces the same digest. Otherwise, Eve could replace Alice’s message to Bob with a completely fabricated one, and Bob would be none the wiser. This is also called weak collision resistance.

The third property is called strong collision resistance. It should be very difficult for Eve to find any two messages that produce the same digest. Otherwise, she could produce one message to be authorized and signed by Alice, then later swap out the message for a malicious one, and everyone would think Alice signed it.

The difference between weak and strong collision resistance is subtle. Pre-image (weak collision) resistance mitigates the discovery of a duplicate digest for an existing message. Strong collision resistance mitigates the discovery of any duplicate digests.

Common CHF Algorithms:

1. NSA’s Secure Hash Algorithms (SHA-1, SHA-2)
2. Ronald Rivest’s MD2, MD4, MD5, and MD6
3. Keccak and its derivatives (SHA-3, KangarooTwelve)

A quick note on vulnerabilities

I list here some common cryptographic hash function families. Some algorithms have been found to be vulnerable to certain kinds of attacks but can still be used in certain cryptographic applications. For example, SHA-1, which we used in our example, is susceptible to practical collision attacks. Therefore, it no longer meets essential property 3 and is deemed “cryptographically broken." It should not be used for any application where collision resistance is essential, like digital signatures. However, it still meets the first two properties, for now, and is still safe to use with Hash-based Message Authentication Codes (HMAC) and in data integrity applications, like git version control. MD2, MD4, and MD5 are all also cryptographically broken in the sense that they have virtually no collision resistance at all. There have also been some demonstrations of pre-image attacks that are faster than brute force. There may still be uses for them in certain applications, but sometimes it’s best to not use cryptographically broken hash functions at all if you aren’t completely confident that the broken properties are not essential for your application. That being said, there may not be any problem at all in using MD5 for non-cryptographic applications, like in hash tables or for identifying changes in version control systems. It is a very fast algorithm.

The Payload Link to heading

Alice already gave Bob the digest for the payload in her secret message. Now with the payload in hand, we can verify its integrity.

Algorithm: SHA-256
Payload Digest: 820a585de241523f7da40c0dcbc42228f39460b3f627d109873952c0e3c83e62

Download the payload here. (Note: the extension is .bin but it’s just a gif image. The extension was changed to avoid image previews spoiling the surprise.)

Try it yourself! Go to https://cryptotools.dev, go to the Digest tab, and drag-and-drop the file into the textarea. Ensure the selected algorithm is SHA-256. Then, click the verify element and paste in the SHA-256 digest. Then click the Verify button.

Verification Result:

true

Okay! So, the payload’s integrity has been verified and we have confidence that it has not been manipulated by Eve.

There is just one more concern, however… When Alice is ready, how will she give her orders to Bob? How can Bob trust that the orders really came from Commander Alice, and not from Eve pretending to be Alice?

With a digital signature.

Authenticity Link to heading

Earlier I mentioned that Public Key Encryption isn’t very effective at encrypting large amounts of data very quickly. Symmetric algorithms are much better. That being said, asymmetric keys are mathematically intertwined. If I give my public key to the whole world, anyone can use it to encrypt a message. But only the private key can decrypt it, and only I have the private key.

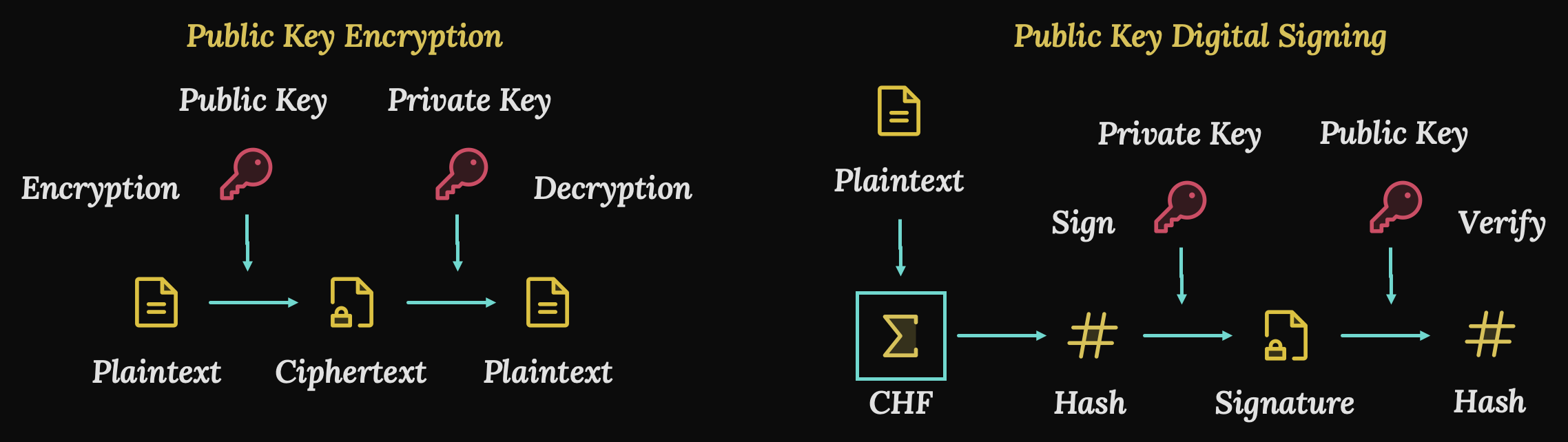
The private key can also be used to encrypt a message, which the public key can decrypt. This is called a digital signature and can be used to authenticate a message. It works like this: The message is passed through a one-way, Cryptographic Hash Function, which we talked about earlier. The hash function outputs a fixed-length set of bits which are then encrypted using the private key. The ciphertext in this case is called a digital signature. The message and the signature are then sent to the recipients, who have the public key. Anyone with the public key can decrypt the digital signature to recover the digest. Then they can hash the message to verify that the digests are the same. This proves that the message is authentic, because only the private key could have produced the signature, and it is presumably held by just one person.

The Command Link to heading

Bob has received Alice’s command. It’s time to break into the central media station and upload the payload. It must be deployed at 0600. But what if it’s a trap? How can Bob be sure that Eve didn’t fabricate this message, pretending to be Alice?

The message was signed, so it includes a digital signature. Everyone knows Alice’s public key, so all Bob needs to do is verify it. Let’s do that now.

Message:  DEPLOY THE PAYLOAD AT 0600
Algorithm:  Elliptic Curve Digital Signature Algorithm with curve P-256
Hash Function:  SHA-256
Signature:  iMmtNXnP+1fDFWwjmAN9C9glJvW3jPAyPLevm4dTksL028sJ/RJ80HtHmVrOoVXP+fpWGx0n9rQzDdGxqySt6Q==

Alice’s Public Key (PEM encoded):

-----BEGIN PUBLIC KEY-----
MFkwEwYHKoZIzj0CAQYIKoZIzj0DAQcDQgAExSNjMSfypOrTln5fdWXTI0iEdXzGlqzkclEE6jcxoPOSnF7ohhDQ1DTei2I70K45B1mIENewvyRivKxZoNCiDw==
-----END PUBLIC KEY-----

Try verifying the message yourself! Go to https://cryptotools.dev > Encryption > Import Key. Check the “Save Locally” box if you want the key to persist through page refreshes. Then click Import. Select the newly imported key from the key list, then paste the message and the signature into their respective fields. Leave the hash function as SHA-256. Then click Verify.

Verification Result:

true

Good, Alice did send the command! Time to get busy. Bob makes his way under the cover of early dawn to the central media station, sneaks past the guards, and locates the mainframe. (Every hacker story needs a mainframe.)

He’s In Link to heading

He connects the payload and waits for it to broadcast across the city on every display. “I hope this works or I’m dead meat,” he thinks to himself.

Never gonna let you down Link to heading

Alas, after a few minutes, he hears a thump. And then another. He quietly leaves the room and tiptoes to the source of the sounds. It seems to be a gathering area for the replicants.

“The payload worked!” Bob exclaimed. The captivating visual sequence has successfully negated their lifespan values, resulting in immediate retirement. Cryptography has saved the day and liberated Los Angeles from the replicants!

CryptoTools Link to heading

In addition to saving the day and all of humanity, CryptoTools has a lot of neat features. Play around with it on your own at https://cryptotools.dev.

Footnotes Link to heading

I’m not a mathematician or a cryptologist. If you found an error, please let me know and I’ll correct it. Furthermore, if you found an error in CryptoTools, please open an issue.

All Blade Runner style imagery in this blog post was generated by DALL•E.

Why Alice, Bob, and Eve? These are common names used in the cryptography world. Alice and Bob are the entities A and B communicating with one another. Eve is the eavesdropper in between.